Ed's
AV Handbook
Batting practice for the AV Professional
and primer for the novice
Chapter 7 Page 2
An Acoustical Strategy
for the
small room
The 4 acoustical regions of the small room
The 'Master Handbook of Acoustics'
offers a strategy that divides the small room into four regions,
each matched to a dedicated mix of tactics to cope with
acoustical-distortion. The following augments their
tactics with well-known acoustical-principles plus practical
solutions garnered from my colleagues over four decades.
Computation Notes:
Speed of sound = 1130ft/sec
L = Longest Dimension
Primary mode = 1/2 the speed of sound ÷ room dimension
Primary mode harmonics = multiples of the primary mode.
Computation Notes:
Speed of sound = 1130ft/sec
L = Longest Dimension
Primary mode = 1/2 the speed of sound ÷ room dimension
Primary mode harmonics = multiples of the primary mode.
1. Region of long wavelengths
The 1st region consists of
wavelengths that are longer than the primary mode of the
longest room dimension: > 565 ÷ L. This region is not
affected by small room acoustics. Some mistakenly
believe that this region establishes the lowest frequency a
room can reproduce. That is not true. In this
region, the room dimensions do not impart any resonant support
or affect.
Acoustical tactic for the 1st region
Leave this region alone.
Acoustical tactic for the 1st region
Leave this region alone.
2. Region dominated by room modes
The 2nd region consists of
wavelengths shorter than the primary axial mode of the longest
dimension but longer than 1.9 feet, the wavelength of 300Hz.
Room mode harmonics peaks, and nulls.
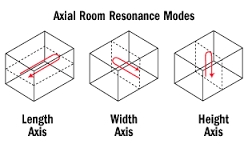
F1 represents the primary axial mode of each opposite room boundary -- height, width, length.The wavelengths of F1 are equal to 1/2 the speed of sound divided by its dimension.
Each of the three primary axial modes produces resonating harmonics.
The 1st harmonic of each primary mode is F2. F2 is equal to F1 x 2.
The 2nd harmonic F3 is equal to F1 x 3. The 3rd harmonic F4 is equal to F1 x 4, which is followed by F5, F6, F7, and so on.
The three primary axial modes and their harmonics produce peaks and nulls, acoustical swells, throughout the small room.
-- F1 peaks at its opposite boundaries;
but nulls at the mid-point of the room dimension.
-- F2 peaks at its opposite boundaries, and at the mid-point of the dimension;
but nulls at the mid-point between each peak.
-- F3 peaks at its opposite boundaries, the mid-point and 1/4 and 3/4 points of the dimension;
but nulls at the mid-point between each peak.
-- F(x) This peak/null 'swell' behavior continues with each succeeding harmonic.
Adjacent modes primaries + harmonics
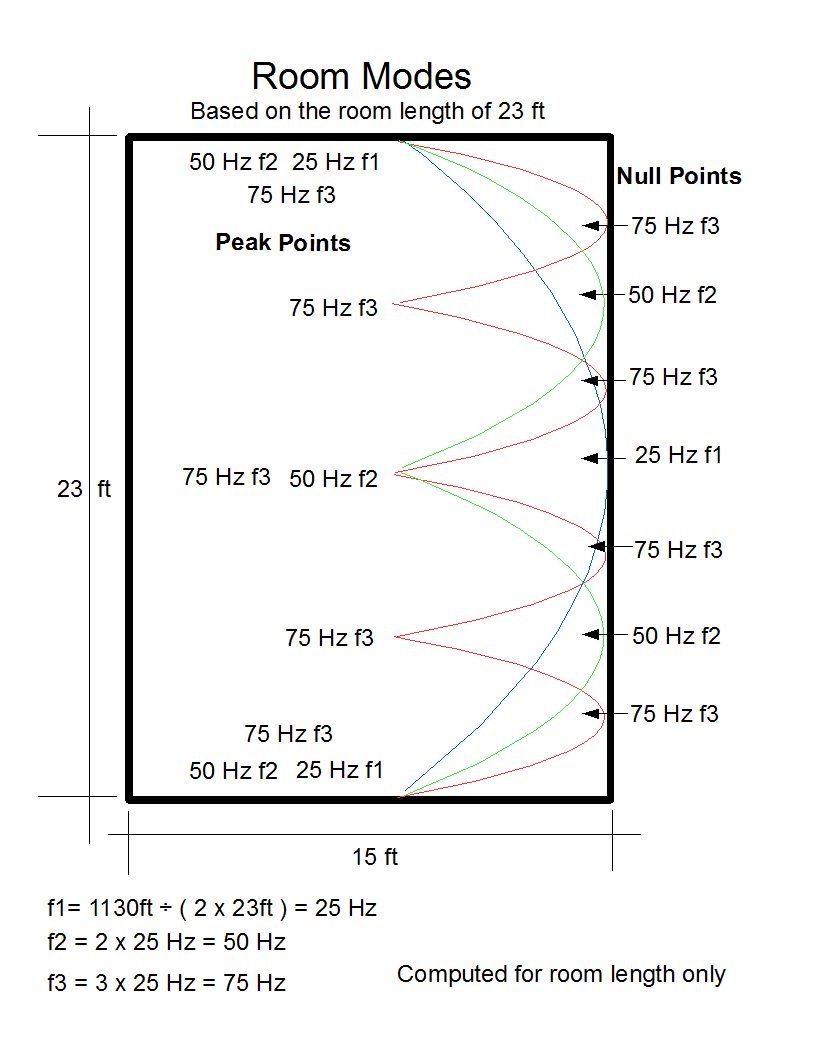
From approximately 565÷L to 300Hz, adjacent modes [ of all 3 primaries and their harmonics] with a coincidence or large spacing create distorting peaks and nulls which create deviations from flat frequency response. Coincidences create peaks, while large spacing creates dips or nulls.
-- A
coincidence equals a difference between modes of 5Hz or less.
-- Large
spacing between modes equals approximately 20Hz or more
Above 300Hz their influence is
minimal.
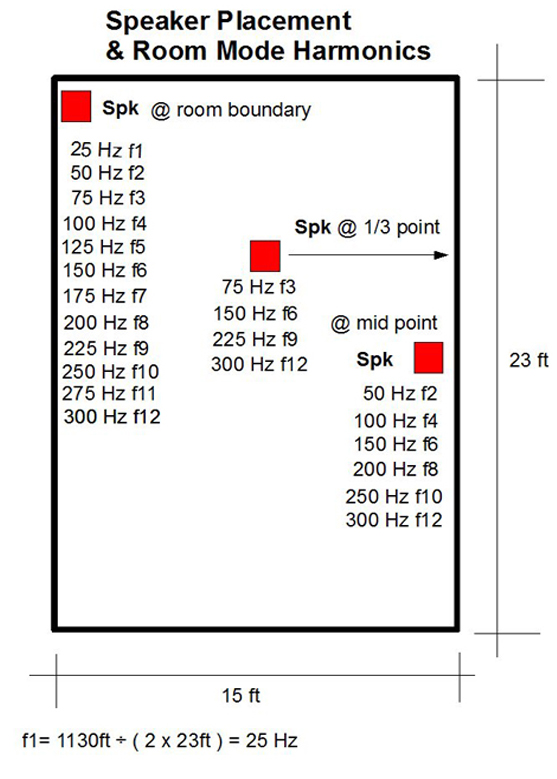
-- A speaker placed at a room boundary excites F1 and all its harmonics.
-- A speaker placed at the mid-point of a dimension stimulates only the even-numbered harmonics of F1.
-- A speaker placed at 1/3 of a dimension stimulates only the 3rd, 6th, 9th, 11th, 14th, etc, harmonics of F1.
-- A speaker placed at 1/4 of a dimension stimulates only the 4th, 8th, 12th, etc, harmonics of F1
-- And the pattern continues.
Speaker placement will be further addressed later in this chapter.
Peaks, Nulls, & Speaker Placement
Speaker placement influences room mode peaks and nulls.-- A speaker placed at a room boundary excites F1 and all its harmonics.
-- A speaker placed at the mid-point of a dimension stimulates only the even-numbered harmonics of F1.
-- A speaker placed at 1/3 of a dimension stimulates only the 3rd, 6th, 9th, 11th, 14th, etc, harmonics of F1.
-- A speaker placed at 1/4 of a dimension stimulates only the 4th, 8th, 12th, etc, harmonics of F1
-- And the pattern continues.
Speaker placement will be further addressed later in this chapter.
Tangential & Oblique Modes
I have avoided tangential and oblique modes, a wave bouncing off more than two opposite boundaries. Their amplitude is a great deal weaker than primary-modes. Fortunately, tangential and oblique modes typically fill-in nulls between the more widely spaced primary modes and their harmonics. Therefore, for this 'small room' discussion, we will assume that their disruptive effect is negligible.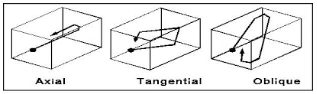
Ed's AV Handbook
Copyright 2007 Txu1-598-288 Revised 2024
Sponsored By

Architectural Speaker Tuning System
for
in-wall/ceiling custom installed speakers.
Reclaim
The Performance You Paid For
Site Menu
Home
Table of
Contents
Handbook Chapters
1 AV
Terms
2 AV Physics
3 Sound Reproduction
4 Video Reproduction
5 The AV System Sequence
6 The Room, Speaker, & TV
7 Acoustical Strategy - Small Room
8 Home Theater by Design
9 AV Sales Training
10 AV Business & Marketing
Contact
About